Name: _______________________ Date: _____________ Class period: ________

Student Worksheet
Lesson: Reading Graphs with a Logarithmic Scale
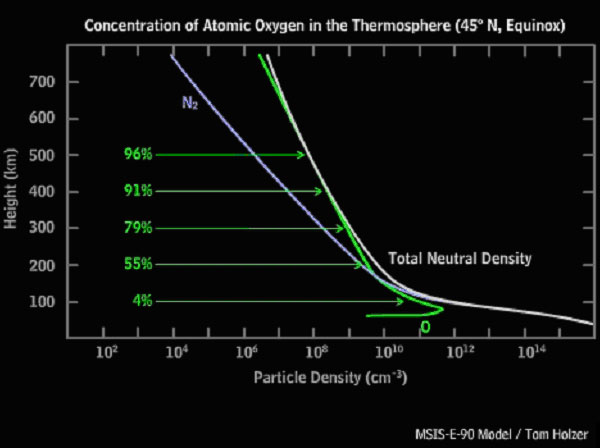
- Carefully observe the x-axis of the above graph, “Concentration of Atomic Oxygen in the Thermosphere”– notice the exponents. These numbers are an abbreviated format used for scientific notation. An example would be: 102 = 1 x 102 = 10 x 10 = 100. In the table below, indicate the actual number represented by the scientific notation.
| Scientific Notation |
102 |
104 |
106 |
108 |
1010 |
| Actual Number |
100 |
- Study the actual numbers along the x-axis.
Do they increase in equal intervals? __________
Is there a pattern to how the x-axis numbers increase? ___________
Explain the pattern that you observe.
- The x-axis is a logarithmic scale, which means that each number is ten times greater than the one before it. An example would be:
| 1 x 10 = 10 (101) 10 x 10 = 100 (102) 100 x 10 = 1000 (103) 1000 x 10 = 10000 (104) |
Logarithmic scales do NOT display equal intervals, as do non-logarithmic scales. Carefully observe the diagram below displaying a logarithmic scale along the x-axis.
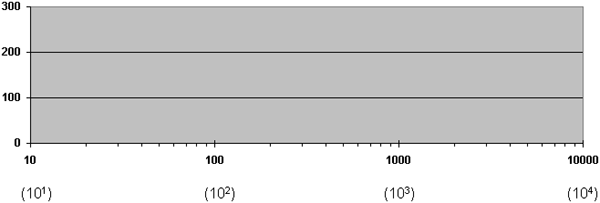
The small marks between the numbers 10 and 100 are 20, 30, 40, 50, 60, 70, 80, and 90 respectively. Notice that they are not evenly spaced.
The small marks between the numbers 100 and 1000 are 200, 300, 400, 500, 600, 700, 800, and 900 respectively.
The uneven spacing is because you are working with the logarithmic function of these actual numbers not the numbers themselves. For example:
| log (10) = 1.00 log (20) = 1.30 log (30) = 1.48 log (40) = 1.60 log (50) = 1.70 |
|
log (60) = 1.78 log (70) = 1.85 log (80) = 1.90 log (90) = 1.95 |
These numbers would all be placed along the x-axis between 101 and 102.
| log (100) = 2.00 log (200) = 2.30 log (300) = 2.48 log (400) = 2.60 log (500) = 2.70 |
|
log (600) = 2.78 log (700) = 2.85 log (800) = 2.90 log (900) = 2.95 |
These numbers would all be placed along the x-axis between
102 and 103.
(Notice that numbers after the decimal point display a consistent
pattern. For example 1.78, 2.78, 3.78, 4.78, etc. will all have a ‘6’ as
the first digit – 60, 600, 6000, and 60,000 respectively. The number
before the decimal indicates how many places are present after the first
digit. For example, 1.78 would start with a ‘6’ and be followed
by one place = 60. Or 3.78 would start with a ‘6’ and be followed
by three places = 6000.)
- Now you try it. For the following logarithm functions of actual numbers, give the logarithm number. Try it first WITHOUT using a calculator, and then check your work using a calculator.
log (1000) = |
log (6000) = |
|||||||
log (2000) = |
log (7000) = |
|||||||
log (3000) = |
log (8000) = |
|||||||
log (4000) = |
log (9000) = |
|||||||
log (5000) = |
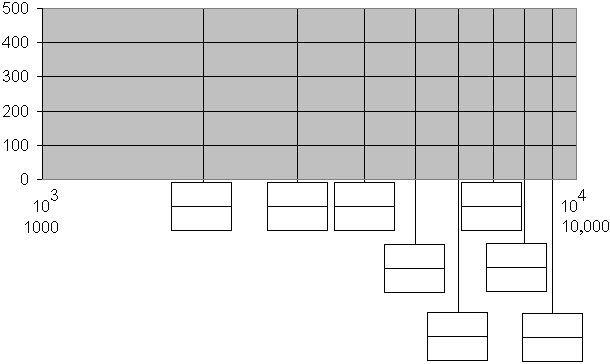
- On the axis below, complete the scale by placing the scientific notation numbers in the top boxes and the actual numbers in the bottom boxes.
- Refer to the graph, “Concentration of Atomic Oxygen in the Thermosphere” as you complete the following data table.
Height (km) /
(% Concentration) |
Particle Density (cm-3) of
Atomic Oxygen (green line) |
100 / ( 4%)
|
|
200 / (55%)
|
|
300 / (79%)
|
|
400 / (91%)
|
|
500 / (96%)
|
- Using the above data, describe in some detail how the concentration of atomic oxygen in the Earth’s thermosphere changes with height. Be sure to include actual and/or logarithmic numbers in your description.
- Consider this: As you go higher in the thermosphere from 100 km to 500 km, the percentage of atomic oxygen increases from 4% to 96%, but the concentration of particle density per cubic centimeter decreases. Why do you think this happens?
You will need to keep this spacing of a logarithmic scale in mind as you complete data tables in two other lessons: "Graphs and the Composition of Earth’s Thermosphere" and "Graphs and the Composition of Earth’s Ionosphere".
Last modified July 18, 2006 by Randy Russell.
© 2011 National Earth Science Teachers Association. Windows to the Universe® is a registered trademark of NESTA. All Rights Reserved.