Haz "click" en la imagen para una vista completa
Animación de Randy Russell (miembro del equipo de Ventanas al Universo).
Órbitas elípticas
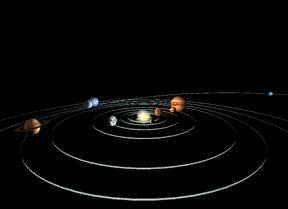
Es posible que creas que la mayoría de los objetos que orbitan alrededor de algo se mueven en círculos, pero este no es el caso. Aún cuando los objetos siguen órbitas circulares, la mayoría de las órbitas tienen forma de cículos u óvalos "estirados hacia afuera". A esta forma ovalada, los matemáticos y astrónomos la llaman, elipse. Todos los planetas de nuestro sistema solar, gran cantidad de satélites, y la mayoría de las lunas, se desplazan a lo largo de órbitas elípticas.
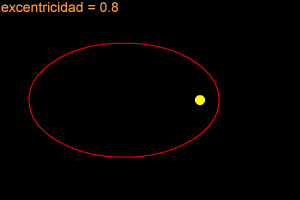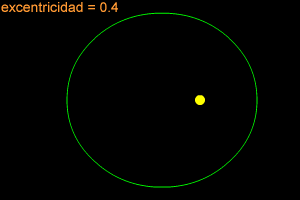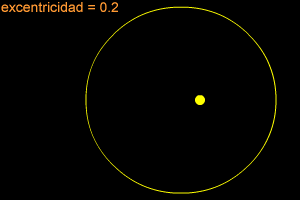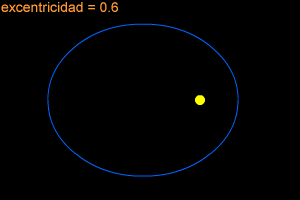
Una elipse puede ser muy larga y delgada, también puede ser bastante redonda -casi como un círculo. Para describir cuán redonda y "estirada hacia afuera" es una elipse, los científicos se refieren a ella con el término especial, "excentricidad". Si la excentricidad de una elipse se encuentra cerca de 1 (como 0.8 ó 0.9), la elipse es larga y delgada. Si la excentricidad está cerca de cero, entonces la elipse es casi un círculo.
La Tierra se mueve alrededor del Sol en una órbita elíptica. La órbita de la Tierra es practicamente un círculo perfecto, ¡su excentricidad es de sólo 0.0167! Plutón tiene la órbita menos circular de todos los planetas del sistema solar. La órbita de Plutón tiene una excentricidad de 0.2488.
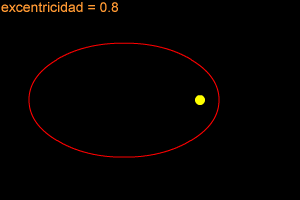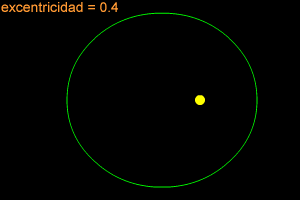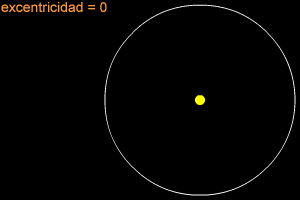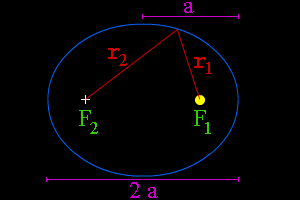
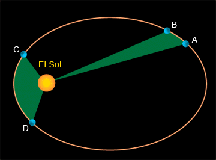
El Sol no se encuentra totalmente en el ecntro de la órbita elíptica de ningún planeta. Una elpise tiene un punto un poco alejado del centro llamado, "focus". Esto se debe a que el Sol se encuentra en el focus de la elipse. Debido a que el Sol está en el focus, y no en el centro o en la elipse, el planeta se acerca y se aleja en cada órbita del Sol. El punto cercano de cada órbita se llama, perihelio. El punto lejano se llama, afelio.
Johannes Kepler un astrónomo alemán que vivió en el siglo 17, descubrió algunas leyes importantes acerca de las órbitas. La Primera ley de movimiento planetario de Kepler, indica que los planetas se mueven en órbitas elípticas. La Segunda ley de Kepler explica cómo los planetas se mueven más rapidamente cuando se acercan al Sol (cerca del perihelio), que cuando se encuentran lejos (cerca de afelio).
Si deseas saber más acerca de la matemática de las elipses, ve al nivel "Avanzado" de esta página.